This article originally appeared in the February 1999 issue of Scientific American.  For a copy of it, please contact Scientific American at 212.754.0550.  We highly recommend a subscription to this important magazine. A Multifractal Walk Down Wall Street "The geometry that describes the shape of coastlines and the patterns of galaxies also elucidates how stock prices soar and plummet." by Benoit B. Mandelbrot Individual investors and professional stock and currency traders know better than ever that prices quoted in any financial market often change with heart-stopping swiftness. Fortunes are made and lost in sudden bursts of activity when the market seems to speed up and the volatility soars. Last September, for instance, the stock for Alcatel, A French telecommunications equipment manufacturer, dropped about 40 percent one day and fell another 6 percent over the next few days. In a reversal, the stock shot up 10 percent on the fourth day. The classical financial models used for most of this century predict that such precipitous events should never happen. A cornerstone of finance is modern portfolio theory, which tries to maximize returns for a given level of risk. The mathematics underlying portfolio theory handles extreme situations with benign neglect:   it regards large market shifts as too unlikely to matter or as impossible to take into account.  It is true that portfolio theory may account for what occurs 95 percent of the time in the market. But the picture it presents does not reflect reality, if one agrees that major events are part of the remaining 5 percent. An inescapable analogy is that of a sailor at sea. If the weather is moderate 95 percent of the time, can the mariner afford to ignore the possibility of a typhoon? The risk-reducing formulas behind portfolio theory rely on a number of demanding and ultimately unfounded premises. First, they suggest that price changes are statistically independent of one another: for example, that today’s price has no influence on the changes between the current price and tomorrow’s. As a result, predictions of future market movements become impossible. The second presumption is that all price changes are distributed in a pattern that conforms to the standard bell curve. The width of the bell shape (as measured by its sigma, or standard deviation) depicts how far price changes diverge from the mean; events at the extremes are considered extremely rare. Typhoons are, in effect, defined out of existence. Do financial data neatly conform to such assumptions? Of course, they never do. Charts of stock or currency changes over time do reveal a constant background of small up and down price movements – but not as uniform as one would expect if price changes fit the bell curve. These patterns, however, constitute only one aspect of the graph. A substantial number of sudden large changes – spikes on the chart that shoot up and down as with the Alcatel stock – stand out from the background of more moderate perturbations. Moreover, the magnitude of price movements (both large and small) may remain roughly constant for a year, and then suddenly the variability may increase for an extended period. Big price jumps become more common as the turbulence of the market grows – clusters of them appear on the chart. According to portfolio theory, the probability of these large fluctuations would be a few millionths of a millionth of a millionth of a millionth. (The fluctuations are greater than 10 standard deviations.) But in fact, one observes spikes on a regular basis – as often as every month – and their probability amounts to a few hundredths. Granted, the bell curve is often described as normal – or, more precisely, as the normal distribution. But should financial markets then be described as abnormal? Of course not – they are what they are, and it is portfolio theory that is flawed. Modern portfolio theory poses a danger to those who believe in it too strongly and is a powerful challenge for the theoretician. Though sometimes acknowledging faults in the present body of thinking, its adherents suggest that no other premises can be handled through mathematical modeling. This contention leads to the question of whether a rigorous quantitative description of at least some features of major financial upheavals can be developed. The bearish answer is that large market swings are anomalies, individual "acts of God" that present no conceivable regularity. Revisionists correct the questionable premises of modern portfolio theory through small fixes that lack any guiding principle and do not improve matters sufficiently. My own work – carried out over many years – takes a very different and decidedly bullish position. I claim that variations in financial prices can be accounted for by a model derived from my work in fractal geometry. Fractals – or their later elaboration, call multifractals – do not purport to predict the future with certainty. But they do create a more realistic picture of market risks. Given the recent troubles confronting the large investment pools call hedge funds, it would be foolhardy not to investigate models providing more accurate estimates of risk. Multifractals and the Market An extensive mathematical basis already exists for fractals and multifractals. Fractal patterns appear not just in the price changes of securities but in the distribution of galaxies throughout the cosmos, in the shape of coastlines and in the decorative designs generated by innumerable computer programs. A fractal is a geometric shape that can be separated into parts, each of which is a reduced-scale version of the whole. In finance, this concept is not a rootless abstraction but a theoretical reformulation of a down-to-earth bit of market folklore – namely, that movements of a stock or currency all look alike when a market chart is enlarged or reduced so that is fits the same time and price scale. An observer then cannot tell which of the data concern prices that change from week to week, day to day or hour to hour. This quality defines the charts as fractal curves and makes available many powerful tools of mathematical and computer analysis. A more specific technical term for the resemblance between the parts and the whole is self-affinity. This property is related to the better-known concept of fractals called self-similarity, in which every feature of a picture is reduced or blown up by the same ratio – a process familiar to anyone who has ever ordered a photographic enlargement. Financial market charts, however, are far from being self-similar.   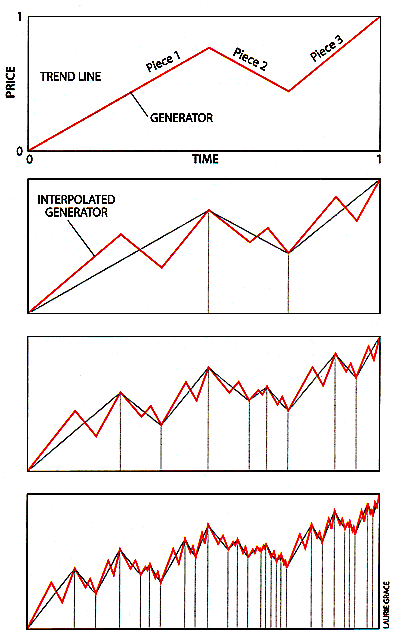Illustration 1 - THREE-PIECE-FRACTAL GENERATOR (top) can be interpolated repeatedly into each piece of subsequent charts (bottom three diagrams).  The pattern that emerges icreasingly resembles market price oscillations.  (The interpolated generator is inverted for each descending piece.)         In a detail of a graphic in which the features are higher than they are wide – as are the individual up-and-down price ticks of a stock – the transformation from the whole to a part must reduce the horizontal axis more than the vertical one. For a price chart, this transformation must shrink the time-scale (the horizontal axis) more than the price scale (the vertical axis). The geometric relation of the whole to its parts is said to be one of self-affinity. The existence of unchanging properties is not given much weight by most statisticians. But they are beloved of physicists and mathematicians like myself, who call them invariances and are happiest with models that present an attractive invariance property. A good idea of what I mean is provided by drawing a simple chart that inserts price changes from time 0 to a later time 1 in successive steps. The intervals themselves are chosen arbitrarily; they may represent a second, an hour, a day or a year. The process begins with a price, represented by a straight trend line (illustration 1). Next, a broken line called a generator is used to create the pattern that corresponds to the up-and-down oscillations of a price quoted in financial markets. The generator consists of three pieces that are inserted (interpolated) along the straight trend line. (A generator with fewer than three pieces would not simulate a price that can move up and down.) After delineating the initial generator, its three pieces are interpolated by three shorter ones. Repeating these steps reproduces the shape of the generator, or price curve, but at compressed scales.  Both the horizontal axis (timescale) and the vertical axis (price scale) are squeezed to fit the horizontal and vertical boundaries of each piece of the generator.   Interpolations Forever Only the first stages are shown in the illustration, although the same process continues. In theory, it has no end, but in practice, it makes no sense to interpolate down to time intervals shorter than those between trading transactions, which may occur in less than a minute. Clearly, each piece ends up with a shape roughly like the whole. That is, scale invariance is present simply because it was built in. The novelty (and surprise) is that these self-affine fractal curves exhibit a wealth of structure — a foundation of both fractal geometry and the theory of chaos. A few selected generators yield so-called unifractal curves that exhibit the relatively tranquil picture of the market encompassed by modern portfolio theory. But tranquillity prevails only under extraordinarily special conditions that are satisfied only by these special generators. The assumptions behind this oversimplified model are one of the central mistakes of modern portfolio theory. It is much like a theory of sea waves that forbids their swells to exceed six feet. The beauty of fractal geometry is that it makes possible a model general enough to reproduce the patterns that characterize portfolio theory’s placid markets as well as the tumultuous trading conditions of recent months. The just described method of creating a fractal price model can be altered to show how the activity of markets speeds up and slows down — the essence of volatility. This variability is the reason that the prefix "multi-" was added to the word "fractal." To create a multifractal from a unifractal, the key step is to lengthen or shorten the horizontal time axis so that the pieces of the generator are either stretched or squeezed. At the same time, the vertical price axis may remain untouched. In illustration 2, the first piece of the unifractal generator is progressively shortened, which also provides room to lengthen the second piece. After making these adjustments, the generators become multifractal (M1 to M4). Market activity speeds up in the interval of time represented by the first piece of the generator and slows in the interval that corresponds to the second piece (illustration 3). Such an alteration to the generator can produce a full simulation of price fluctuations over a given period, using the process of interpolation described earlier. Each time the first piece of the generator is further shortened — and the process of successive interpolation is undertaken — it produces a chart that increasingly resembles the characteristics of volatile markets (illustration 4). The unifractal (U) chart shown here (before any shortening) corresponds to the becalmed markets postulated in the portfolio theorists’ model. Proceeding down the stack (M1 to M4), each chart diverges further from that model, exhibiting the sharp, spiky price jumps and the persistently large movements that resemble recent trading. To make these models of volatile markets achieve the necessary realism, the three pieces of each generator were scrambled — a process not shown in the illustrations. It works as follows: imagine a die on which each side bears the image of one of the six permutations of the pieces of the generator. Before each interpolation, the die is thrown, and then the permutation that comes up is selected. What should a corporate treasurer, currency trader or other market strategist conclude from all this? The discrepancies between the pictures painted by modern portfolio theory and the actual movement of prices are obvious. Prices do not vary continuously, and they oscillate wildly at all timescales. Volatility — far from a static entity to be ignored or easily compensated for — is at the very heart of what goes on in financial markets. In the past, money managers embraced the continuity and constrained price movements of modern portfolio theory because of the absence of strong alternatives. But a money manager need no longer accept the current financial models at face value. Instead multifractals can be put to work to "stress-test" a portfolio. In this technique the rules underlying multifractals attempt to create the same patterns of variability as do the unknown rules that govern actual markets. Multifractals describe accurately the relation between the shape of the generator and the patterns of up-and-down swings of prices to be found on charts of real market data. On a practical level, this finding suggests that a fractal generator can be developed based on historical market data. The actual model used does not simply inspect what the market did yesterday or last week. It is in fact a more realistic depiction of market fluctuations, called fractional Brownian motion in multifractal trading time. The charts created from the generators produced by this model can simulate alternative scenarios based on previous market activity. These techniques do not come closer to forecasting a price drop or rise on a specific day on the basis of past records. But they provide estimates of the probability of what the market might do and allow one to prepare for inevitable sea changes. The new modeling techniques are designed to cast a light of order into the seemingly impenetrable thicket of the financial markets. They also recognize the mariner’s warning that, as recent events demonstrate, deserves to be heeded: On even the calmest sea, a gale may be just over the horizon. Pick the Fake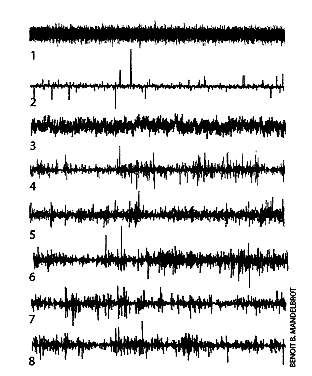 How do multifractals stand up against actual records of changes in financial prices? To assess their performance, let us compare several historical series of price changes with a few artificial models. The goal of modeling the patterns of real markets is certainly not fulfilled by the first chart, which is extremely monotonous and reduces to a static background of small price changes, analogous to the static noise from a radio. Volatility stays uniform with no sudden jumps. In a historical record of this kind, daily chapters would vary from one another, but all the monthly chapters would read very much alike. The rather simple second chart is less unrealistic, because is shows many spikes; however, these are isolated against an unchanging background in which the overall variability of prices remains constant. The third chart has interchanged strengths and failings, because it lacks any precipitous jumps. The eye tells us that these three diagrams are unrealistically simple. Let us now reveal the sources. Chart 1 illustrates price fluctuations in a model introduced in 1900 by French mathematician Louis Bachelier. The changes in prices follow a "random walk" that conforms to the bell curve and illustrates the model that underlies modern portfolio theory. Charts 2 and 3 are partial improvements on Bachelier’s work: a model I proposed in 1963 (based on Levy stable random processes) and one I published in 1965 (based on fractional Brownian motion). These revisions, however, are inadequate, except under certain special market conditions. In the more important five lower diagrams of the graph, at least one is a real record and at least another is a computer-generated sample of my latest multifractal model. The reader is free to sort those five lines into the appropriate categories. I hope the forgeries will be perceived as surprisingly effective. In fact, only two are real graphs of market activity. Chart 5 refers to the changes in price of IBM stock, and chart 6 shows price fluctuations for the dollar-deutsche mark, exchange rate. The remaining charts (4, 7 and 8) bear a strong resemblance to their two real-world predecessors. But they are completely artificial, having been generated through a more refined form of my multifractal model. -B.B.M.   The Author Benoit B. Mandelbrot has contributed to numerous fields of science and art. A mathematician by training, he has served since 1987 as Abraham Robinson Professor of Mathematical Sciences at Yale University and IBM Fellow Emeritus (Physics) at the Thomas J. Watson Reasearch Center in Yorktown Heights, N.Y., where he worked from 1958 to 1993. He is a fellow of the American Academy of Arts and Sciences and foreign associate of the U.S. National Academy of Sciences and the Norwegian Academy. His awards include the 1993 Wolf Prize for physics, the Barnard, Franklin and Steinmetz medals, and the Science for Art, Harvey, Humboldt and Honda prizes.   Further Reading The Fractal Geometry of Nature. Benoit B. Mandelbrot. W.H. Freeman and Company, 1982. Fractals and Scaling in Finance: Discontinuity, Concentration, Risk. Benoit B. Mandelbrot. Springer-Verlag, 1997. "The Multifractal Model of Asset Returns." Discussion papers of the Cowles Foundation for Economics, Nos. 114-1166. Laurent Calvert, Adlai Fisher and Benoit B. Mandelbrot. Cowles Foundation, Yale University, 1997. Multifractals and 1/F Noise: Wild Self-Affinity in Physics. Benoit B. Mandelbrot, Springer-Verlag, 1999.